A Particle Filtering Framework for Prognosis

The generation of long-term predictions of a fault indicator entails large-grain uncertainty. For that reason, we believe that accurate and precise prognosis of a failing component/ subsystem must consider critical state variables as random variables with associated probability distributions. Particularly, our research focuses on estimating and predicting the evolution of a fault (or fault indicator) using an approach that combines information from both stochastic fault growth state models and on-line measurement data. Fault growth models are assumed to be nonlinear to accurately represent the underlying dynamics of the physical system, and also non-Gaussian to represent complex uncertainties and disturbances.

Recursive Bayesian estimation approaches allow incorporating measurement data as sequential observations, as well as modifying “a priori” state estimate by considering the likelihood of those observations. Sequential Monte Carlo methods – also referred to as Particle Filtering – are especially useful in the presence of model nonlinearities or non-Gaussian noise assumptions, since they solve the estimation problem numerically. Unlike classical Monte Carlo methods, Particle Filtering uses the principle of importance sampling (IS) to represent density functions with random samples and a set of associated weights. Thereby, the variance of integration in the Bayesian update equation is reduced and the number of samples required to approximate the distributions with necessary precision is optimized.

Under this approach, prognosis is based on both an adaptive fault progression model and an accurate Particle Filter estimate of the current state. Both pieces of information allow predicting the trend of fault evolution in time and therefore the probability of failure if load conditions are maintained. As new data becomes available, long-term predictions are updated and a learning correction-based procedure is used to improve both their accuracy and precision.

Typical outcomes of the prognosis module include 95% confidence interval and expectations for the Remaining Useful Life (RUL) of the component under study. Customer specifications are included in the form of hazard thresholds for the system under analysis, statistical confidence level and minimum required prediction window.

Last but not least, the issue of uncertainty in some of the parameters of the fault progression model is incorporated in our scheme, by considering those parameters as additional states of a generalized system (which need to be estimated as process data streams in). In that sense, the Particle Filter approach allows to handle the existence of noisy measurements and uncertainties in model parameters simultaneously

References

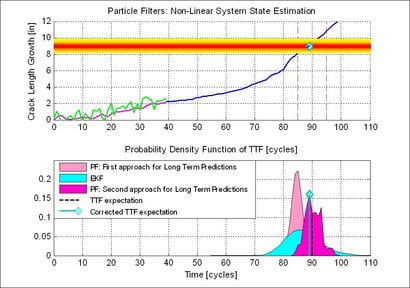
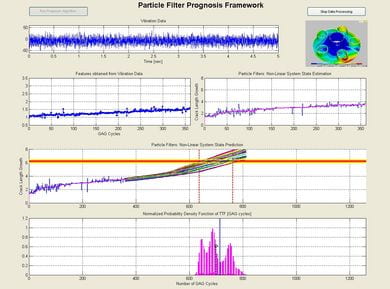
A brief description of the proposed PF prognosis approach.

“A Particle Filtering-based Framework for On-line Fault Diagnosis and Failure Prognosis,” Ph.D. Thesis Proposal, Georgia Institute of Technology, approved on October 2006.

Orchard, M., Wu, B., and Vachtsevanos, G., “A Particle Filter Framework for Failure Prognosis,” Proceedings of WTC2005, World Tribology Congress III, Washington D.C., USA, 2005.